Concept of the differential. A number of notations are used to represent the derivative of the function y = f(x): Dxy, y', f '(x), etc. However, the notation most commonly used is dy/dx. Here a fractional notation is employed, dy as numerator and dx as denominator. One might well wonder why this fractional notation is used. The derivative is not defined as a fraction. It is defined as a number, a limit. Why use a fractional notation? The truth is, it is often convenient to view the derivative as a fraction. It is defined as the limit
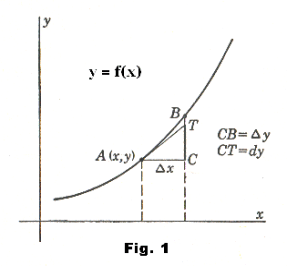
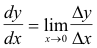
and it is often thought of as the fraction Δy/Δx where Δx is a very small increment. In fact, in this fractional notation dy and dx are really modified abbreviations for Δy and Δx. Indeed, when one gets into integral calculus one discovers that dx and dy are thought of as separate entities — actually the entities Δy and Δx, for very small increments of Δx. Thought of in this way, as distinct entities, dx and dy are called differentials. The entity dx is conceived of as a small increment, Δx, and dy is defined as dy = f '(x)dx. See Fig. 1. Let us start at any point A(x, y) on the curve and let x increase by a small amount Δx. The corresponding increment in y is given by CB = Δy. The differential dy corresponds to CT. We see that Δy = dy + TB. One can see that if Δx is small TB approaches zero and dy is a good approximation to Δy. This fact is utilized in solving a certain class of problems.
Example. Compute approximately the volume of metal in a hollow spherical shell with a thickness of 0.06 inches and inside radius of 7 inches.
Solution. The volume of metal in our hollow spherical shell is equal to the amount by which the volume increases when its radius increases from to 7.06 in. The volume v of a sphere of radius r is given by
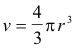
Taking the derivative with respect to r we get
dv/dr = 4π r2
Treating dv/dr as a fraction, we write
dv = 4πr2dr
In our problem r = 7 inches and dr = 0.06 inches. Thus
dv = 4π(49)(0.06) = 36.9 cu. in.
Note that in this example the differentials dr and dv are treated as separate entities and manipulated algebraically as variables.
Differential formulas. The rules and formulas for differentiation are often given in terms of differentials. A table follows. They are often easier to remember and use in this form.
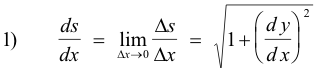
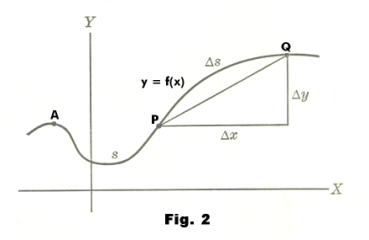 Derivative of arc length. Consider a curve in the x-y plane which, at least over some section of interest, can be represented by a function y = f(x) having a continuous first derivative. Let A be some fixed point on the curve and denote by s the arc length from A to any other arbitrary point P(x, y) on the curve. Let Q be a point at coordinates (x + Δx, y + Δy). See Fig. 2. Denote by Δs the arc length from P to Q. Then the instantaneous rate of change of arc length s per unit change in x is given by
Derivative of arc length. Consider a curve in the x-y plane which, at least over some section of interest, can be represented by a function y = f(x) having a continuous first derivative. Let A be some fixed point on the curve and denote by s the arc length from A to any other arbitrary point P(x, y) on the curve. Let Q be a point at coordinates (x + Δx, y + Δy). See Fig. 2. Denote by Δs the arc length from P to Q. Then the instantaneous rate of change of arc length s per unit change in x is given by
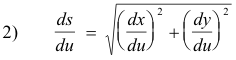
If a curve is given by the parametric equations
x = f(u)
y = g(u)
the rate of change of arc length s with respect to u is given by
Note that both equations 1) and 2) can be derived from the following fundamental relationship:
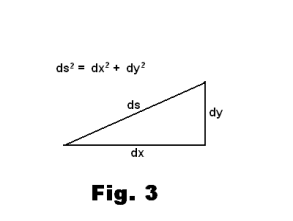
3) ds2 = dx2 + dy2
See Fig. 3. The relationships 1), 2) and 3) are important, much used forms. The relationship
ds2 = dx2 + dy2
reveals that ds is the hypotenuse of a right triangle with edges dx, and dy, a fact which is intuitively obvious since the arc Δs approaches the chord PQ as the chord approaches zero.
If we are dealing with arcs in three dimensional space instead of the plane, 3) becomes
4) ds2 = dx2 + dy2 + dz2
where ds is the diagonal of a rectangular parallelepiped (or box) with edges dx, dy and dz.
Curvature. Intuitively the curvature of a plane curve at a point P can be thought of as the curvature of that circle which approximates the curve most closely near that point. The curvature of a circle is directly defined by the length of its radius. The shorter the radius, the greater the curvature of the arc in the vicinity of any point P on it. The longer the radius, the bigger the circle, and the less the curvature of the arc in the vicinity of any point P on it. For a very large circle the curvature of an arc at some point P approaches that of a straight line i.e. zero curvature. In the following we will give the technical definition of curvature. We will find that this definition leads directly to the result that the curvature, K, of a circle is equal to the reciprocal of its radius r i.e. K = 1/r. Thus, for a circle, the length of its radius is a direct measure of its curvature.
Technical definition of curvature.
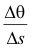 Consider any smooth curve. Curvature measures the rate at which the tangent line turns per unit distance moved along the curve. Or, more simply, it measures the rate of change of direction of the curve.
Consider any smooth curve. Curvature measures the rate at which the tangent line turns per unit distance moved along the curve. Or, more simply, it measures the rate of change of direction of the curve.
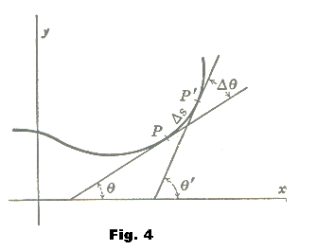
Let P and P' be two points on a curve, separated by an arc of length Δs. See Fig. 4. Then the average curvature of the arc from P to P' is expressed by the fraction
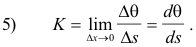
where Δθ = θ'- θ is the angle turned through by the tangent line moving from P to P'. The curvature K at point P is defined as
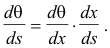
To find dθ/ds we use the formula
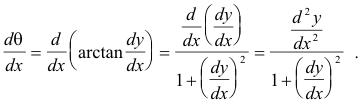
To compute dθ/dx first observe that tan θ = dy/dx so θ = arctan(dy/dx). Consequently,
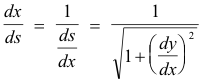
The quantity dx/ds is given by
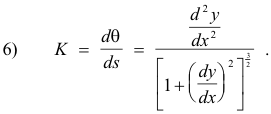
so the formula for curvature is
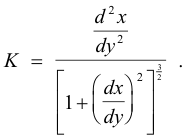
The sign of K will be positive if d2y/dx2 is positive and negative if it is negative. Many authors, however, regard the curvature as the absolute value of K, thus considering curvature as always positive.
Alternate formula for curvature. An alternate formula for curvature is
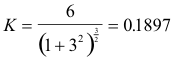
This formula can be used at a point where dy/dx doesn’t exist such as a point on a curve where the tangent line is parallel to the y-axis.
Example. Find the curvature of the cubical parabola y = x3 at (1, 1).
Solution.
dy/dx = 3x2
d2y/dx2 = 6x
dy/dx]1,1 = 3
d2y/dx2]1,1 = 6
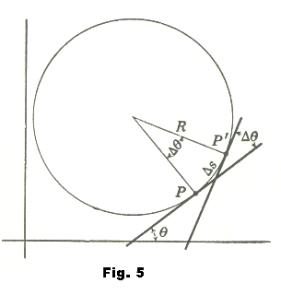
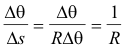 Curvature of a circle. Given a circle of radius R as shown in Fig. 5. The tangent line to the circle at P makes an angle θ with the x-axis. In moving to the position P' it turns through an angle Δθ. The amount of turning per unit distance moved along the arc is
Curvature of a circle. Given a circle of radius R as shown in Fig. 5. The tangent line to the circle at P makes an angle θ with the x-axis. In moving to the position P' it turns through an angle Δθ. The amount of turning per unit distance moved along the arc is
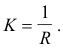
since Δs = RΔθ, θ being measured in radians.
Thus
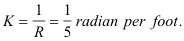
The curvature of a circle is constant and is equal to the reciprocal of the radius.
Example. The curvature of a circle whose radius is 5 ft. is
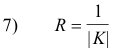
This means that the tangent line, in traversing the circle, turns at a rate of 1/5 radian per foot moved along the arc.
Def. Radius of curvature. The radius of curvature for a point P on a curve is defined as
where K is the curvature.
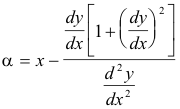
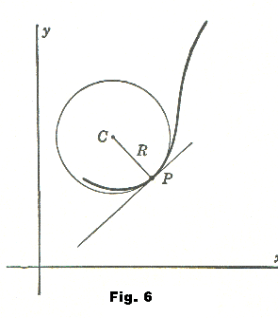
Def. Circle of curvature. Let R be the radius of curvature at a point P on a curve. The circle of curvature or Osculating Circle of the curve at point P is the circle of radius R lying on the concave side of the curve and tangent to it at P. See Fig. 6.
To construct the circle of curvature: On the concave side of the curve construct the normal at P and on it lay off PC = R. The point C is the center of the required circle.
The circle of curvature of a curve at a point P is that particular circle which has the same curvature as the curve itself at point P. Of the indefinitely large number of circles that can be drawn tangent to the curve at P, this is the only one whose curvature is the same as that of the curve at the point of contact. It can be shown that this circle “fits” the curve more closely in the neighborhood of P than any other circle — just as the tangent line fits it more closely than any other line.
Another definition of the circle of curvature at point P is as follows: Suppose we pass a circle through P and two arbitrarily selected neighboring points P' and P'' on the curve. The limiting position of this circle as P' and P'' both approach P along the curve can be shown to be identical with that of the circle of curvature as defined above.
Center of curvature. The center of curvature for a point P(x, y) of a curve is the center C of the circle of curvature at P. The coordinates (α, β) of the center of curvature are given by
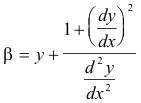
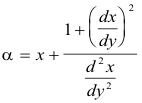
or
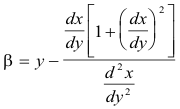
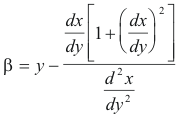
Def. Evolute. The evolute of a curve is the locus of the centers of curvature of a given curve.

and it is often thought of as the fraction Δy/Δx where Δx is a very small increment. In fact, in this fractional notation dy and dx are really modified abbreviations for Δy and Δx. Indeed, when one gets into integral calculus one discovers that dx and dy are thought of as separate entities — actually the entities Δy and Δx, for very small increments of Δx. Thought of in this way, as distinct entities, dx and dy are called differentials. The entity dx is conceived of as a small increment, Δx, and dy is defined as dy = f '(x)dx. See Fig. 1. Let us start at any point A(x, y) on the curve and let x increase by a small amount Δx. The corresponding increment in y is given by CB = Δy. The differential dy corresponds to CT. We see that Δy = dy + TB. One can see that if Δx is small TB approaches zero and dy is a good approximation to Δy. This fact is utilized in solving a certain class of problems.
Example. Compute approximately the volume of metal in a hollow spherical shell with a thickness of 0.06 inches and inside radius of 7 inches.
Solution. The volume of metal in our hollow spherical shell is equal to the amount by which the volume increases when its radius increases from to 7.06 in. The volume v of a sphere of radius r is given by
Taking the derivative with respect to r we get
dv/dr = 4π r2
Treating dv/dr as a fraction, we write
dv = 4πr2dr
In our problem r = 7 inches and dr = 0.06 inches. Thus
dv = 4π(49)(0.06) = 36.9 cu. in.
Note that in this example the differentials dr and dv are treated as separate entities and manipulated algebraically as variables.
Differential formulas. The rules and formulas for differentiation are often given in terms of differentials. A table follows. They are often easier to remember and use in this form.
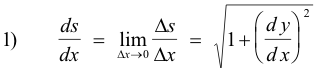

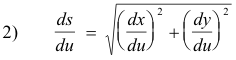
If a curve is given by the parametric equations
x = f(u)
y = g(u)
the rate of change of arc length s with respect to u is given by


Note that both equations 1) and 2) can be derived from the following fundamental relationship:
3) ds2 = dx2 + dy2
See Fig. 3. The relationships 1), 2) and 3) are important, much used forms. The relationship
ds2 = dx2 + dy2
reveals that ds is the hypotenuse of a right triangle with edges dx, and dy, a fact which is intuitively obvious since the arc Δs approaches the chord PQ as the chord approaches zero.
If we are dealing with arcs in three dimensional space instead of the plane, 3) becomes
4) ds2 = dx2 + dy2 + dz2
where ds is the diagonal of a rectangular parallelepiped (or box) with edges dx, dy and dz.
Curvature. Intuitively the curvature of a plane curve at a point P can be thought of as the curvature of that circle which approximates the curve most closely near that point. The curvature of a circle is directly defined by the length of its radius. The shorter the radius, the greater the curvature of the arc in the vicinity of any point P on it. The longer the radius, the bigger the circle, and the less the curvature of the arc in the vicinity of any point P on it. For a very large circle the curvature of an arc at some point P approaches that of a straight line i.e. zero curvature. In the following we will give the technical definition of curvature. We will find that this definition leads directly to the result that the curvature, K, of a circle is equal to the reciprocal of its radius r i.e. K = 1/r. Thus, for a circle, the length of its radius is a direct measure of its curvature.
Technical definition of curvature.
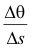
Let P and P' be two points on a curve, separated by an arc of length Δs. See Fig. 4. Then the average curvature of the arc from P to P' is expressed by the fraction
where Δθ = θ'- θ is the angle turned through by the tangent line moving from P to P'. The curvature K at point P is defined as
To find dθ/ds we use the formula
To compute dθ/dx first observe that tan θ = dy/dx so θ = arctan(dy/dx). Consequently,
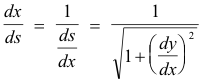
The quantity dx/ds is given by
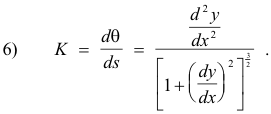
so the formula for curvature is
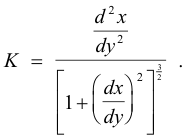
The sign of K will be positive if d2y/dx2 is positive and negative if it is negative. Many authors, however, regard the curvature as the absolute value of K, thus considering curvature as always positive.
Alternate formula for curvature. An alternate formula for curvature is
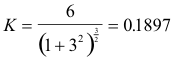
This formula can be used at a point where dy/dx doesn’t exist such as a point on a curve where the tangent line is parallel to the y-axis.
Example. Find the curvature of the cubical parabola y = x3 at (1, 1).
Solution.
dy/dx = 3x2
d2y/dx2 = 6x
dy/dx]1,1 = 3
d2y/dx2]1,1 = 6

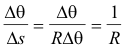
since Δs = RΔθ, θ being measured in radians.
Thus
The curvature of a circle is constant and is equal to the reciprocal of the radius.
Example. The curvature of a circle whose radius is 5 ft. is
This means that the tangent line, in traversing the circle, turns at a rate of 1/5 radian per foot moved along the arc.
Def. Radius of curvature. The radius of curvature for a point P on a curve is defined as

where K is the curvature.
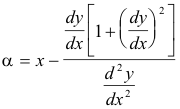
Def. Circle of curvature. Let R be the radius of curvature at a point P on a curve. The circle of curvature or Osculating Circle of the curve at point P is the circle of radius R lying on the concave side of the curve and tangent to it at P. See Fig. 6.
To construct the circle of curvature: On the concave side of the curve construct the normal at P and on it lay off PC = R. The point C is the center of the required circle.
The circle of curvature of a curve at a point P is that particular circle which has the same curvature as the curve itself at point P. Of the indefinitely large number of circles that can be drawn tangent to the curve at P, this is the only one whose curvature is the same as that of the curve at the point of contact. It can be shown that this circle “fits” the curve more closely in the neighborhood of P than any other circle — just as the tangent line fits it more closely than any other line.
Another definition of the circle of curvature at point P is as follows: Suppose we pass a circle through P and two arbitrarily selected neighboring points P' and P'' on the curve. The limiting position of this circle as P' and P'' both approach P along the curve can be shown to be identical with that of the circle of curvature as defined above.
Center of curvature. The center of curvature for a point P(x, y) of a curve is the center C of the circle of curvature at P. The coordinates (α, β) of the center of curvature are given by
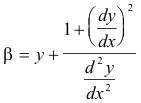
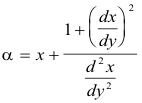
or
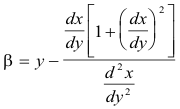
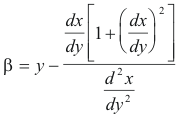
Def. Evolute. The evolute of a curve is the locus of the centers of curvature of a given curve.

No comments:
Post a Comment